Érdekes weboldalak
Egy kis humor

Egy minneapolisi házaspár eldöntötte, hogy Floridába megy felmelegedni egy különösen fagyos télen. Úgy tervezték, hogy ugyanabban a hotelben szállnak meg, ahol a mézesheteiket töltötték 20 évvel azelőtt.
Mozgalmas programjuk miatt nehéz volt összeegyeztetni az utazási időpontot, ezért a férj pénteken, a feleség pedig a következő napon repült Minneapolisból Floridába.
A férj bejelentkezett a hotelbe, ahol a hotelszobában egy számítógép is volt, nem úgy mint évekkel azelőtt, és eldöntötte, hogy küld egy e-mailt feleségének. Véletlenül azonban kihagyott az e-mail címből egy betűt, s anélkül, hogy észrevette volna a tévedést, elküldte a levelet a rossz címre.
***************************************************
Közben ... valahol Houstonban ... egy özvegy épp a férje temetéséről érkezett haza, akit az Úr hazahívott az Ő dicsőségébe, egy szívinfarktus után. Az özvegy elhatározta, hogy megnézi a barátoktól és rokonoktól érkezett e-maileket. Miután elolvasta az üzenetet, visított és elájult. Fia berohant a szobába, édesanyját a földön találta, majd felpillantott a képernyőn található szövegre:
"Szerető feleségemnek
Időpont: 2013. nov.22., péntek
Tárgy: megérkeztem!
Drága szerelmem!
Tudom, meg vagy lepődve, hogy üzenetet kapsz tőlem. Már számítógépük is van az ittenieknek és lehet szeretteinknek e-mailt küldeni.
Épp most érkeztem meg és jelentkeztem be. Minden elő van készítve a holnapi érkezésedre és már nagyon várom, hogy találkozzunk.
Remélem, hogy az utazásod olyan csendes lesz, mint az enyém.
Ui.: Tényleg nagyon meleg van idelent !!! "

Kedves Péter!
Örömmel értesítelek, hogy szerelmünk gyümölcse, a kis Péter, megszületett. Sajnos anyatejem nem lévén szoptató-dajkát kellett alkalmaznom. Ő kubai származású, így a tejétől gyermekünk bőre szinte teljesen fekete lett. Erről ugyebár én abszolúte nem tehetek ...
A te szerető Anitád
Drága édesanyám!
Az imént vettem kézhez Anita levelét, melyben értesít, hogy kisfiúnk született. Mivel nincs elég anyateje dajka segítségére szorul, aki színes bőrű, és a tejétől kis unokád bőre is csaknem fekete lett, amiről persze az én drágám egyáltalán nem tehet. Remélem te is együtt örülsz velünk.
Ölel fiad, Péter
Édes fiam!
A te születésedkor én pontosan ugyanúgy jártam, mint most a te Anitád. Elapadt a tejem, ezért téged tehéntejjel kellett tápláljalak. Valószínűleg ettől lettél te ekkora marha ... Amiről persze én egyáltalán nem tehetek.
Csókol Anyád

Az idős kis hölgy egy nap bement a kanadai nemzeti bankba egy táskányi pénzzel. Ragaszkodott hozzá, hogy a bank elnökével kíván beszélni számlanyitással kapcsolatban, mondván: Sok pénzről van szó! Kevés hümmögés és hezitálás után a bank személyzete odakísérte az elnök irodájához az asszonyt. Az elnök megkérdezte, mennyit is szándékozik a bankban letétbe helyezni. 165.000 dollárt. - felelte a hölgy, és a táskájából kiborította a pénzt az íróasztalra. Az elnök természetesen rögtön kíváncsi lett, honnan származik a pénz és megkérdezte:
- Asszonyom, meglepett mekkora összegű készpénzzel rendelkezik....Megtudhatnám, honnan van a pénz?
- Fogadásokból. - felelte az asszony.
- Miféle fogadásokból? - kérdezte az elnök.
- Hát, például fogadok önnel 25.000 dollárba, hogy az ön heréi szögletesek. - felelte az idős hölgy.
- Hahaha - nevetett az elnök - Ez egy idióta fogadás. Ilyen fogadást az életben nem nyerhet meg.
- Tartja esetleg a fogadást? - kérdezte kihívóan a hölgy.
- Persze! - fogadok 25.000 dollárba, hogy a heréim nem szögletesek!
- Mivel jelentős összegről van szó - mondta az idős hölgy - lehetséges, hogy holnap reggel 10 órára visszatérjek az ügyvédemmel, mint tanúval?
- Természetesen - felelte az elégedett elnök.
Aznap este az elnök rendkívül ideges volt a fogadás miatt, jelentős időt töltött a tükör előtt, ellenőrizve golyóit, forgatva jobbra - balra, újra meg újra. Gondosan ellenőrizte mindaddig, amíg teljességgel meg nem győződött arról, hogy semmiképp sem lehetnek szögletesek a golyói, és meg fogja nyerni a fogadást.
Másnap reggel pontosan 10 órakor az idős kis hölgy megjelent az elnök irodájában az ügyvédjével. Bemutatta az ügyvédet az elnöknek, majd megismételte a fogadást:
- 25.000 dollárt arra, hogy az elnök golyói szögletesek!
Az elnök elfogadta a fogadást, majd a hölgy megkérte, hogy vesse le a nadrágját, hogy mindannyian láthassák. Az elnök megtette. A kis idős hölgy egész közelről rámeredt a herékre, majd megkérdezte, hogy lehet-e megfognia?
- Nos, rendben - felelte az elnök. - 25.000 dollár nagy pénz, és szeretném, ha abszolút biztos lenne a dolgában.
Ekkor vette észre, hogy a hölgy ügyvédje csendben elkezdi verni a fejet a falba.
- Mi a fene van az ügyvédjével? - kérdezte az elnök.
- Semmi - felelte a hölgy. - Kivéve azt, hogy tegnap fogadtam vele 100.000 dollárba, hogy ma reggel 10 órakor a kanadai nemzeti bank elnökének a golyói a kezemben lesznek.

A farmer bemegy a városba, hogy bevásároljon.
Vesz a vaskereskedésben egy üllőt, egy vödröt, majd betér az állatkereskedésbe és vesz két csirkét, és egy libát. Amikor el akarja vinni, rájön, hogy ez a sok dolog nem fér el a kezében. Mivel gyalog van, a farm meg messze, ezért leül gondolkodni, mitévő legyen?
A boltos megsajnálja, és a következőt javasolja neki:
- Rakja az üllőt a vödörbe, ezt vigye az egyik kezében, a csirkéket rakja a hóna alá, a másik kezében pedig el tudja vinni a libát. A farmer megörül, felpakol, és elindul.
Ahogy kiér a város határába, látja, hogy egy fiatal, nagymellű szőke, kékszemű szépség álldogál az úton. A lány megkérdi tőle:
- Meg tudja nekem mondani, hogy jutok a Mockingbird Lane 1515-be?
- Nos, hölgyem, én a Mockingbird Lane 1516-ba megyek, az ott van nem messze. Jöjjön velem, tudok egy rövidebb utat az erdőn keresztül.
- Hohó! és mi a biztosíték arra, hogy az erdőben nem támad le, nem dönt neki egy fának, nem tépi le a blúzomat és nem erőszakol meg?
- Látja, hölgyem, hogy egy üllő, egy vödör, két csirke és egy liba van nálam! Ugyan, hogy tudnám én így megerőszakolni?
- Hááát... Mondjuk leteszi a libát a földre, letakarja a vödörrel, ráteszi az üllőt, a csirkéket pedig megfognám én...

Néhány hónappal ezelőtt a CIA-nál üresedés volt egy merénylői állásra. Igen nehéz egy ilyen beosztásra megfelelő embert találni, és a jelentkezőknek jó néhány teszten és ellenőrzésen kell átesni, mielőtt egyáltalán szóba kerülhetnek, mint jelöltek. Miután néhány jelentkezőt leellenőriztek, gyakorlatoztattak és leteszteltek, két férfira és egy nőre szűkítették le a jelentkezők körét, de csak egy emberre volt szükségük. Elérkezett az utolsó próbatétel napja, ahol végre kiderül majd, ki kapja meg a titkos állást. A CIA emberei, akik a tesztet vezették, egy hatalmas fémajtóhoz vezették az egyik férfit, és adtak neki egy pisztolyt.
- Tudnunk kell, hogy követi az utasításokat, függetlenül a körülményektől - magyarazták. - Ebben a szobában ott ül egy széken a felesége. Fogja ezt a fegyvert, és ölje meg!
A férfi döbbenten nézett rájuk:
- Ezt nem mondhatják komolyan! Soha nem tudnám lelőni a feleségem!
- Nos - mondta a CIA egyik embere -, maga egyértelműen nem a megfelelő ember erre a munkára. így aztán odaviszik a másik férfit az ajtóhoz, és odanyújtják neki a fegyvert.
- Tudnunk kell, hogy függetlenül a körülményektől követi az utasításainkat - magyarázták a második embernek. - Odabent ott ül egy széken a felesége. Fogja ezt a pisztolyt, és ölje meg!
A második férfi kissé megdöbbent ezek hallatán, de azért magához vette a fegyvert, és bement a szobába. Teljes csend volt úgy 5 percig, majd kinyílt az ajtó.
- Megpróbáltam, de egyszerűen nem tudtam meghúzni a ravaszt és lelőni a feleségem. Azt hiszem nem én vagyok a maguk embere.
- Valóban nem - felelt a CIA egyik embere. - Maga nem alkalmas erre az állásra. Vigye csak haza a feleségét. Most már csak a nő volt hátra. őt is odavezetik a nagy fémajtóhoz, és odanyújtják neki a pisztolyt.
- Biztosan tudnunk kell, hogy függetlenül a körülményektől, követni fogja az utasításainkat. Ez az utolsó teszt. Odabent ott ül egy széken a férje. Fogja ezt a fegyvert, és ölje meg.
A nő elvette a fegyvert, és benyitott a szobába. Amint becsukódott az ajtó, a CIA emberei vad fegyverropogást hallottak. összesen 13 lövést. Aztán elszabadult a pokol a szobában. Sikoltozást, verekedést hallottak és dörömbölő hangokat a falakon. Ez jónéhány percig ment így, aztán hirtelen csend lett. Az ajtó lassan kinyílt, és ott állt előttük a nő. Letörölte az izzadságot a homlokáról, és így szólt:
- Hé fiúk, nem mondták, hogy a pisztolyban vaktöltények vannak! A székkel kellett agyonvernem az átkozottat!

- Hová ilyen sietősen?
- Ne is kérdezze biztos úr! Most lőttem le az anyósomat, itt a hullája a csomagtartóban. A csőre töltött pisztolyt még nem volt időm eldobni, itt van a kesztyűtartóban.
A rendőr döbbenten előrántja a pisztolyát s a sofőrre fogja, a másik kezével meg rádión sürgős segítséget kér. Megjön az erősítés.
- Mire volt a nagy riadó, őrmester?
- Hadnagy úr, jelentem, ennek az egyénnek ott az anyósa lelőve a csomagtartóban, a pisztoly meg a kesztyűtartóban!
Átvizsgálják a kocsit se hulla, se pisztoly, semmi különöset nem találnak. Egyszer csak megszólal a sofőr:
- Fogadjunk, most még azt is rám fogja majd, hogy kétszázzal száguldozok!

Teletömött 56-os villamos, két, egymással szemben lévő szék. Az egyiken egy jóarcú, kedves öreg néni kuporog, a másikon egy nő a gyerekével az ölében. A kissrác himbálja a lábát, és állandóan belerúg a néni térdébe. Az öregasszony egyre hátrébb húzódik, várja, hogy az anya mikor szól rá a kölyökre. De mivel ez nem történik meg, udvariasan megszólítja az anyát:
- Elnézést, hogy zavarom, de a kisfia folyamatosan rugdossa a lábamat, és ez már az én koromban nem tréfa, eltalál egy csontot, vagy egy eret, akkor az újságosig, meg a patikáig se tudok lemenni. Legyen szíves szóljon rá!
- Mit akar? - reccsen rá az anya -, én nem fogom egy ilyen vénasszony miatt korlátozni a gyerekemet testi szabadságában! Foglalkozzon a saját dolgával, ne az én gyerekemmel!
A villamoson mindenki megdöbbenéssel nézi végig a jelenetet, míg egy tipikus rocker (acélbetétes, tar frizura, feszülős gatya, bőr kabát, fülében üvölt a Tankcsapda) kiveszi a szájából a rágót, és a paraszt nő hajába gyönyörűen beledolgozza, majd lágyan így szól:
- Engem se korlátoztak gyerekkoromban!

Két hete volt a 45. születésnapom. Egyébként sem éreztem magam valami fényesen. Lementem reggelizni. A feleségem azt sem mondta: Jó reggelt, nemhogy Isten éltessen. A gyerekek sem mondtak semmit, teljesen hidegen hagytam őket. úton az irodába már teljesen levert voltam.
Bementem az ajtón és Janet, a titkárnőm felállt és így szólt: Isten éltesse sokáig, főnök! Na, ettől egy kicsit mindjárt jobban lettem. Legalább egy valaki nem felejtett el! Délig dolgoztam. Pontban 12-kor Janet bekopogott az ajtómon és azt mondta:
- Főnök, ma van a születésnapja. Menjünk el ebédelni, csak mi ketten! Nem a szokásos étterembe mentünk, hanem egy hangulatos kis falusi lokálba, hogy egy kicsit magunk lehessünk. Ittunk két Martinit és elégedettek voltunk a kiváló ételekkel.
A visszaúton Janet azt mondta:
- Tudja, olyan szép ez a mai nap, és ma van a születésnapja. Ne menjünk vissza az irodába! Menjünk fel hozzám és igyuk meg ott a délutáni kávét! Így felmentünk a lakására és kávé helyett megittunk még két Martinit és kényelmesen elszívtunk egy-egy cigarettát.
Egy idő után Janet így szólt:
- Ha önt nem zavarja, felveszek valami kényelmesebbet. Csak beszaladok a hálóba, azonnal itt vagyok. Néhány perc múlva valóban jött is. A kezében egy születésnapi torta volt és őt követték: a feleségem, a gyerekeim és a közelebbi munkatársaink és a Happy Birthday-t énekelték. És én ott ültem a heverőn, és ....... a zoknimon kívül semmi nem volt rajtam!
Családfa kutatás
Indíttatás

A családi biblia üres lapjaira feljegyzett családi események (születések és elhalálozások) dátumai. Itt találtam ükszüleim Gaál Imre és Szabó Eszter, valamint 11 gyermekük adatait, ami elindított őseim keresése, a családfa kutatás felé.

A nagypiriti református anyakönyv második kötetének első lapjai a felújított lelkészlakban - MDCCXCVII (1797). Az amerikai mormon egyház mikrofilmre tette ezen anyakönyveket, így (regisztráció után) könnyen kutatható.
Anyakönyvtípusok

Bolla Vince volt nagypiriti lelkész születési anyakönyve - Noszlop, 1912.08.29.

Gaál Antal és Hajmási Erzsébet házassági anyakönyve - 1796.02.01. "Fordítása":
Anno 1796
Febr.1. Gaál Antal kopuláltatott Nagypiriti Hajmási Péternek hajadon leányával Erzsébettel. Kérő emberek voltak Vecsi János és Hajmási István.

Barthalos Mihály volt nagypiriti lelkész halotti anyakönyve - 1894.01.15. Mára már ledőlt síremléke a nagypiriti temetőben található.
Általam fejlesztett oldalak
Burján Károly - nyög/nyugdíjas
Ez a saját weboldalam ill. oldalaim. Időnként szépítgetem, bővítem a tartalmát és "modernizálom". A site rengeteg zömmel saját készítésű fényképet tartalmaz, amelyeket többféleképpen tudunk megjeleníteni. Fontosabb újdonságok: tudáspróba, ingyenes webtanfolyamok, családi anyakönyvek, stb.
Készült: talán 2008 (első verzió)
Módosítás folyamatosan!
Nagypirit - története
... A községi bíró a kis- és nagyközségek első tisztviselője, a községi elöljáróság feje, a községi képviselő-testület elnöke volt Magyarországon 1950-ig. Írott forrásokból megállapítható, hogy a jobbágysorban élő falusi közösségek már az 1780-as években sok helyen rendesen szabályozott közigazgatási életet éltek, melyben a bírónak vezető szerepe volt. ...
Készült: 2010
Utolsó módosítás: 2022
Lőrinte - Domján János helytörténész gyűjtése
Volt egyszer egy falu, Tósok és Kolontár közt félúton, a Torna patak mentén. Az emberi butaság eltüntette, lakóit szétszórta, földjeit vízzel árasztotta el, kastélyát lerombolta. Ennek állít emléket az oldal. Domján János, volt lőrintei lakos, sok éves munkával rengeteg anyagot gyűjtött levéltárakból és régi lőrinteiektől. (Az eredeti oldal: www.lorinte.org/ címen volt.)
Készült: 2010
Utolsó módosítás: 2022
BIG - Bródy-Net
... Egyik tanítványom, Stocker Vilmos és Timföldgyárban dolgozó édesapja közvetítésével jutottunk az akkor csodaszámba menő programozható HP zsebszámológépekhez. A 41CV típusú gép memóriája 2 kbyte, rendelkezik alfanumerikus billentyűzettel, gördíthető, egysoros alfanumerikus kijelzővel, mágneskártyás háttértárral (a mágneskártya olyan, mint egy lapos rágógumi), pici hőnyomtatóval. Az igazi csoda a géphez kapcsolható csíkkódot (pl. csíkkódban írt program) olvasni tudó fényceruza. Két ilyen (akkor vagyont érő) masinát kaptunk szakkörre a Timföldgyár Irányítástechnikai Főosztályának vezetőjétől, Horváth Istvántól. ...
Készült: 2003
Utolsó módosítás: 2022
BIG - Jubileumi évkönyv 1953-2003
Volt munkahelyem 2003-ban ünnepelte 50 éves jubileumát. Ekkor készült egy részletes évkönyv a gimnázium történetéről. Tanárok, volt diákok írták le emlékeiket. A weboldalak a jubileumi évkönyv számítógépes megvalósításai, emiatt talán kicsit több is a könyvnél.
Készült: 2005
Módosítva nem volt.
BIG - Jubileumi évkönyv 2003-2013
Az előző évkönyv megjelenése óta eltelt 10 esztendő, a Bródy újra jubilált. Én már nyugdíjasként tettem az új könyvet számítógépen is olvashatóvá. A visszaemlékezéseken kívül sok-sok adat is található az oldalakon: az egyes tanévek fontosabb eseményei, tanulmányi- és sporteredmények és rengeteg fénykép.
Készült: 2014
Módosítva nem volt.
BIG - Végzett diákok adatai, tablói
A program/website a Bródy Gimnázium serverén található. A szöveg alapú adatbázisban megtalálható az összes iskolatípus, az összes végzett osztály és osztályfőnöke, tablóik és a végzett diákok névsora az iskola indulásától (1953) napjainkig. Az adatok közt sokféleképpen kereshetünk, akár egy névtöredék alapján is.
Készült: 2007
Utolsó módosítás: 2019
BIG - Bródy Imre Gimnázium Könyvtára
Az iskola könyvtára szabadpolcos rendszerben működik kb. 150 m2 alapterületen, 40 tanulói férőhellyel, internet hozzáféréssel. A több mint 33.000 dokumentum többsége könyv, de videokazetta, hangkazetta, CD-lemez, CD-ROM és DVD is található.
Készült: 2019-2020
Az oldalt a BIG könyvtárosa módosítja.
Dr. Földvári Béla - szemész szakorvos
Általános szemészeti szakorvosi ellátást végzünk, kiemelten foglalkozunk a gyermekszemészettel. Rendelőinkben a legmodernebb felszereléssel, műszerekkel biztosítjuk a páciensek magas színvonalú vizsgálatát és kezelését. Műszerparkunkat folyamatosan bővítettük, ma már pl. digitális szemfenékvizsgáló készülék, komputeres látótér vizsgáló készülék, többféle ultrahang berendezés, OCT készülék, stb. áll rendelkezésre. A rendelésen többféle lézeres beavatkozást is el tudunk végezni.
Készült: 2016, 2020 új
Már a tulajdonos módosítja!
Dr. Ligetes Melinda - fogszakorvos
A MedDent Fogászati Szolgáltató Kft. weboldala. "Magas szinten nyújtjuk mindazokat a kezeléseket, melyek egy modern rendelőtől elvárhatóak. Az általános fogorvosi beavatkozásokat, implantációt, lézeres terápiákat, digitális diagnosztikai eljárásokat, illetve speciális esztétikai igényeket kielégítő fogászati kezeléseket. Ezenkívül praxisunkban szépészeti beavatkozásokat is végzünk."
Készült: 2018
Utolsó módosítás: 2022
Vér Ferenc - fogtechnikus
Vér Ferenc fogtechnikus weboldala. A honlap a fogászati centrum szolgáltatásait, munkatársait, árait és elérhetőségét mutatja. A fényképgalériában láthatók: a rendelő, a laboratórium, a laboratóriumi munkák képei. Az oldalt bővítettem (2018) a Dzsigoló Apartman "reklámjával", illetve a szállóról készült fényképekkel.
Készült: 2015
Utolsó módosítás: 2020
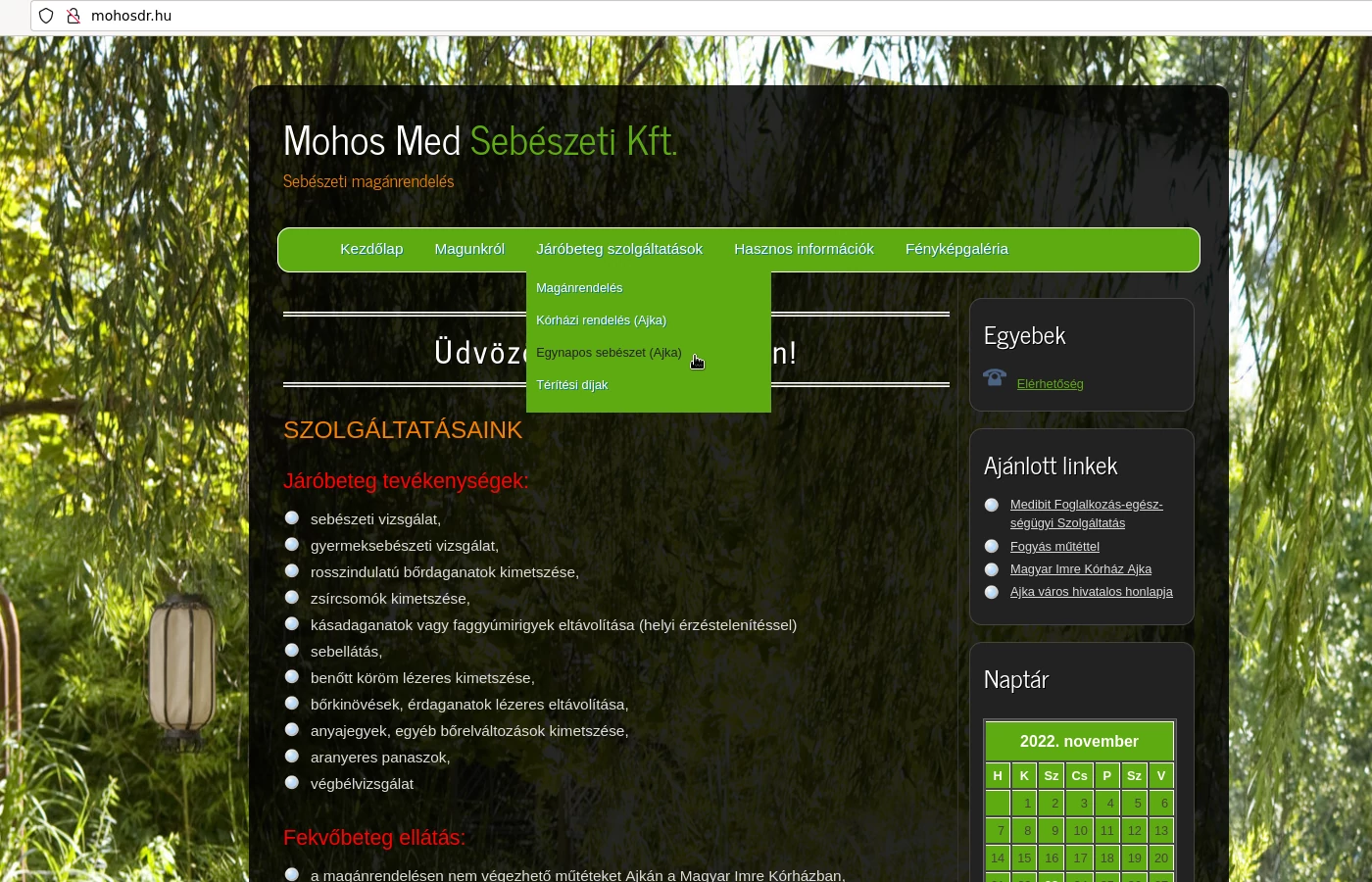
Dr. Mohos György - sebész szakorvos
A 2012-ben létrehozott Mohos Med Sebészeti Kft. weboldala. Fő tevékenyei: sebészeti vizsgálat, rosszindulatú bőrdaganatok, zsír- csomók, anyajegyek, egyéb bőrelváltozások kimetszése, kása- daganatok vagy faggyúmirigyek eltávolítása (helyi érzéstelenítéssel), sebellátás, bőrkinövések, érdaganatok lézeres eltávolítása, végbélvizsgálat, stb.
Készült: 2012
Utolsó módosítás: 2022
Rapi Gábor - Astorkonzorcium Kft.
Cégünk húsz éves múltra tekint vissza a nemzetközi fuvarozás és fuvarszervezés terén. 1993-ban egyéni vállalkozásként kezdte meg működését, 2 db 3,5 tonnás gépjárművel. 1999-ben Kft-vé alakultunk és jelenleg az 1,3t raksúly és a 24t raksúly között minden szállítási igényt ki tudunk elégíteni. 2006-ra elkészült cégünk saját raktárbázisa 1500 m2 polcrendszerrel. Többnyelvű website: magyar, angol, német.
Készült: 2015
Utolsó módosítás: 2020
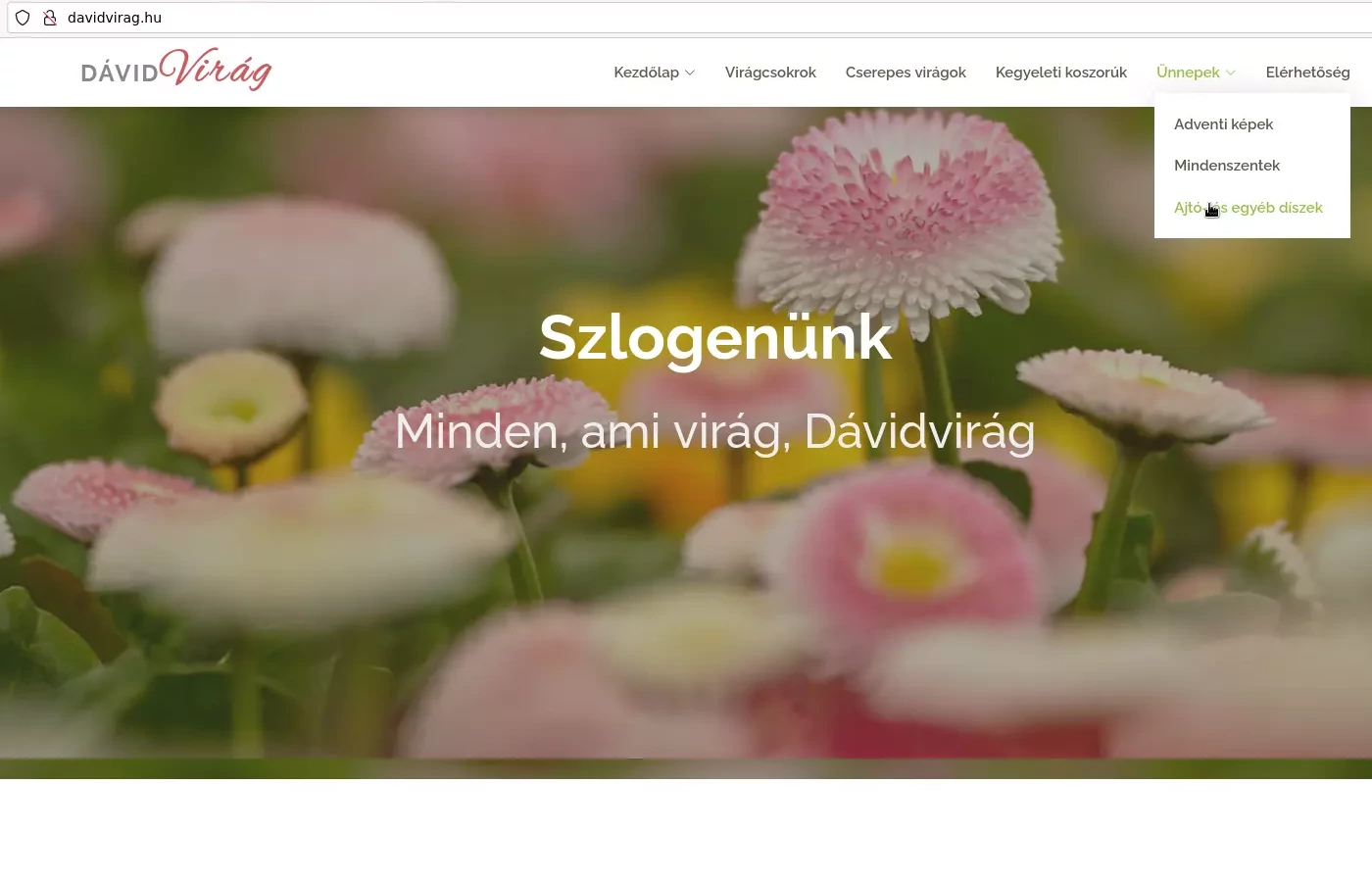
Pintér Dávid - virágkereskedő
2014-ben, Vince napján nyitottuk meg első virágüzletünket Veszprémben, a Vásárcsarnokban. Azóta már széles választékban sok mindent kínálunk:
- születésnapra, névnapra, házassági évfordulóra - virágcsokor, cserepes virág
- anyák napjára, nők napjára, ballagásra - virágcsokor, dekoráció
- esküvőkre - menyasszonyi-, eldobó-, koszorúslány csokor; ruha-, kar-, fejdísz; virágív, teremdekoráció
- temetésre, halottak napjára, megemlékezésre, koszorúzásra - koszorúk és sírcsokrok
Készült: 2022
Utolsó módosítás: 2022
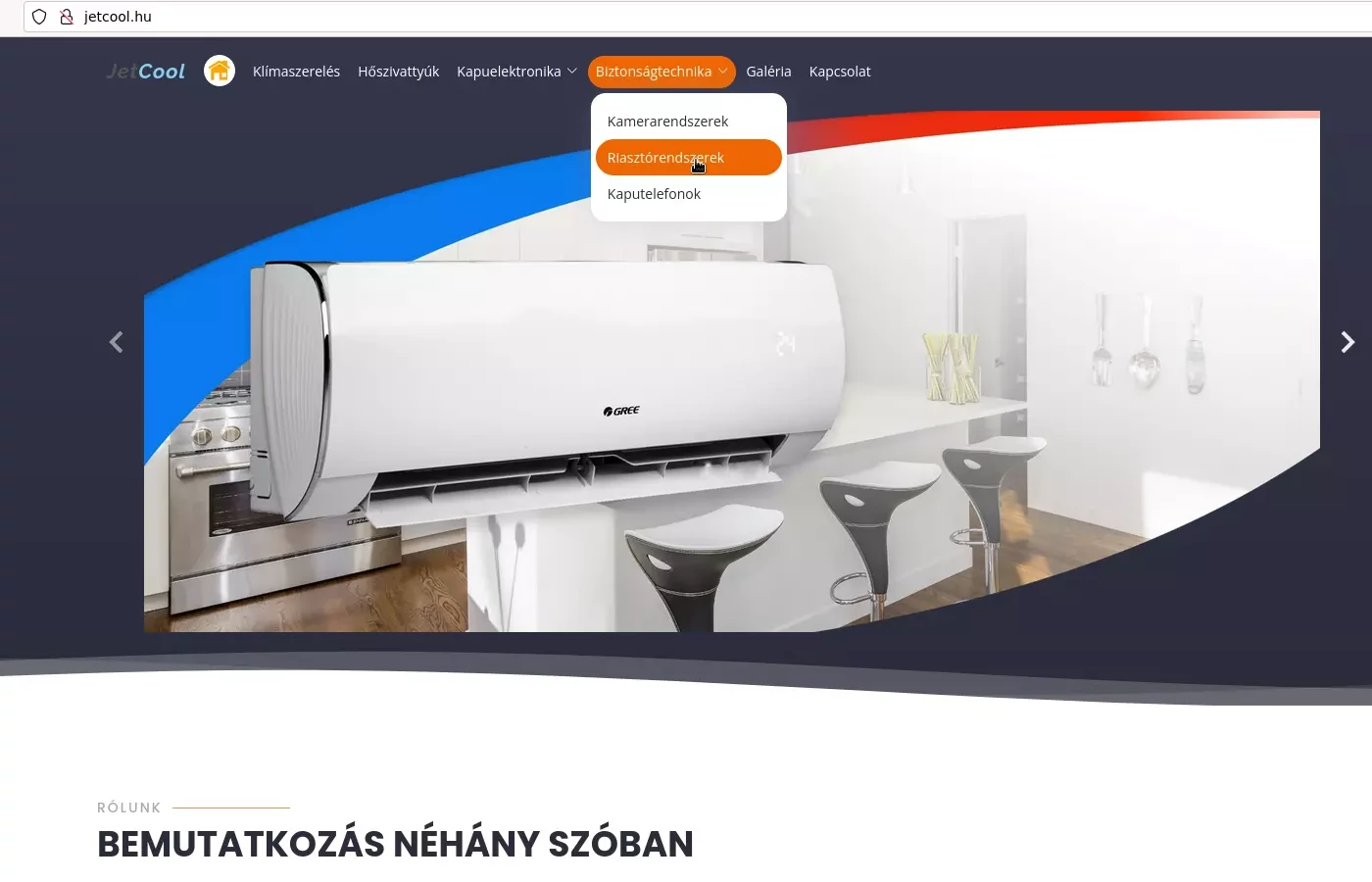
Kőmíves Gergő - klímaszerelő
A JetCool Kft. célja: a lelkiismeretes, korrekt, ügyfélbarát kiszolgálás, ezt szem előtt tartva próbálunk minden munkát szakmaisággal, becsülettel elvégezni. Ismertebb klíma márkákat és kevésbé ismertebbeket egyaránt forgalmazunk és szerelünk, természetesen figyelve az Ön, azaz az ügyfél minden igényére, elképzelésére. Vállaljuk magánszemélyek otthonának, irodák, üzlethelyiségek klimatizálásásnak teljeskörű és profi megoldását. Továbbá vállaljuk a már felszerelt, meglévő klímák karbantartását.
Készült: 2022
Utolsó módosítás: 2022
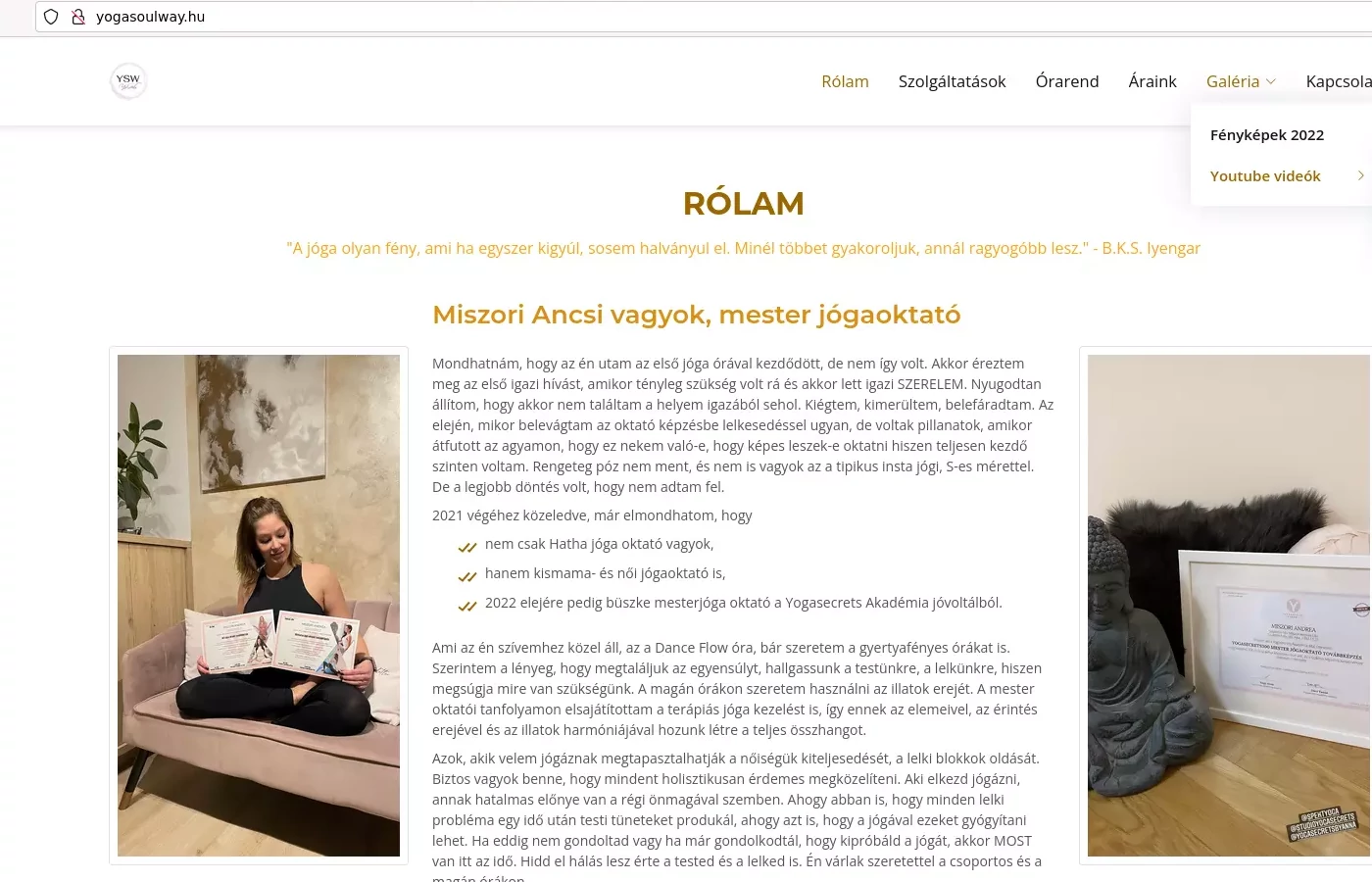
Miszori Andrea - jógaoktató
"Mondhatnám, hogy az én utam az első jóga órával kezdődött, de nem így volt. Akkor éreztem meg az első igazi hívást, amikor tényleg szükség volt rá és akkor lett igazi SZERELEM. Nyugodtan állítom, hogy akkor nem találtam a helyem igazából sehol. Kiégtem, kimerültem, belefáradtam. Az elején, mikor belevágtam az oktató képzésbe lelkesedéssel ugyan, de voltak pillanatok, amikor átfutott az agyamon, hogy ez nekem való-e, hogy képes leszek-e oktatni hiszen teljesen kezdő szinten voltam. ..."
Készült: 2022
Utolsó módosítás: 2022
Tilhof Ágnes - könyvtáros
A Bródy Imre Gimnázium könyvtára szabadpolcos rendszerben az intézmény második emeletén működik kb. 150 m2 alapterületen, 40 tanulói férőhellyel. Több mint 33.000 dokumentummal rendelkezik, mely többsége könyv, de videokazetta, hangkazetta, CD-lemez, CD-ROM és DVD is található. 11 internet hozzáféréssel rendelkező számítógép áll az olvasók rendelkezésére.
Készült: 2019-2023
Utolsó módosítás: 2023
Sulyok Péter - humorista
1986-ban születtem, 2003. július elején vakultam meg teljesen. Ettől kezdve minden egészen új színezetet kapott. Más nézőpontból kellett megvizsgálnom az életem, és döntenem kellett a “lefekszem és elpusztulok (megöl az önsajnálat, vagy az unalom)”, vagy a “felkelek és tovább megyek (küzdelmekkel, fájdalmakkal)” között. Én az utóbbit választottam, révén mindig is harcos lélek voltam.
Készült: 2021
Utolsó módosítás: 2022
Elérhetőség / Kapcsolat
A nagyítható google térképhez kattints a képre!